Naïve Gaussian elimination

Naïve Gaussian elimination is a simple and systematic algorithm to solve linear systems of equations. It is easily introduced by demonstrating with an example. Consider a system of three kinds of fruit (peaches, apples, and bananas). Bags with different numbers of peaches, apples and bananas are weighed and the results are modeled with the following three linear equations.

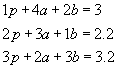
Notice that for cases where there is just one of a kind of fruit we put a coefficient of 1 in front of the variable.

Subtract 2 times equation one from equation two. Replace equation two with the new equation.

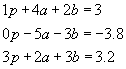
Subtract 3 times equation one from equation three. Replace equation three with the new equation.

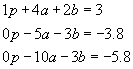
The reason we did this is that now there is a 0 as the first coefficient in equations two and three. The last two equations constitute a two equation system for two unknowns, a and b. We now continue the same procedure. Subtract 2 times equation two from equation three and replace equation three with the new equation.

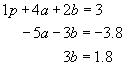
Notice that all operations we used in this process are of the same form: “subtract m times equation i from equation j and replace equation j with this new equation”. Because this rule has he same form for all modifications, this rule can be programmed in computers.

This last form of the system of equations is called upper triangular form. The equations fit into a triangular shape. You can see that this could be done for any system of N equations and N unknowns. The reduction of a general linear system to upper triangular form is the first step of Gaussian elimination and is called forward elimination.

The next step in Gaussian elimination is called back substitution. Use equation three to solve for b. You easily obtain

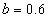
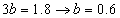
The second equation is solved by using this value to give a = 0.4

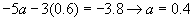
Finally the first equation gives a value for p.

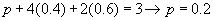
Notice that in the back substitution step, the variables are solved in reverse order.

This algorithm is called naïve Gaussian elimination. The more general Gaussian elimination algorithm for solving linear systems of equations requires a procedure for ordering the equations. This helps to provide numerical accuracy and to detect so-called ill-posed equations.